I wonder, are you at all interested in computational chemistry, or are you only looking at physics? Classical physics? Quantum? Linus Pauling's 1920's publications on the hydrogen molecule in connection to his ideas about quantum theory (in physics) have contributed to what has been happening for twenty years in chemistry: the complete breakdown of all our high school assumptions about how molecular chemistry works.
 |
| old 'stick figure' model of water molecules |
The old 'ball and stick' models of molecular structure that we all remember from high school is a frozen, clunky fiction that doesn't account for the truly dynamic nature of molecular orbits, interactions and bonds. Remember our conversation about that a few months ago—all matter at every level is in a high state of 'agitation', vibrating, and seems quantum rather than fixed? Computational chemistry tries to account for this uncomfortable reality and it uses quantum mechanics (from your discipline, physics) to account for the complexity of a more real
 |
| more real model of carbon! |
 |
| traditional vector calculation |
Classical (or at least high school) chemistry pretends that the predictive power of synthetic and experimental breaking and forming of chemical bonds is based on a fixed structure in molecular reality. You physicists are so pleased with the predictive power and even synthesizing ability of classical computational physics, using computers to predict the future outcomes and experimental outcomes of coherent systems of arbitrary organization with great precision--like magic. You guys can project the future evolution of spiral galaxies and apparent momentum of objects like supernovae in deep field observations; you can track red and blue shifting bodies in distant orbital masses to precision at decimal places--such as vector physics (separations between two moving bodies, rocket arcs, orbital mechanics and so on, such as the basic vector equation: < r2 := (d + (t - T) b Vo) ex + (t - T) c Vo ey - ^"^ 9 ez > to calculate distances between two bodies at time "t", the bodies being whatever, it doesn't matter--the point being that simple equations like this can be used predictively. I got a lot of this from Enns and McGuire, "Computer Algebra Recipes for Classical Mechanics" (Birkhauser, Berlin, 2003). Is it the weak force, electromagnetism, and gravity that lead to this high degree of predictive power in classical physics?
 |
| one-dimensional quantum vectors |
Quantum systems are by contrast radically indeterministic, according to Heisenberg, looking at the strong force, the nuclear force at the most fundamental levels (the dual particle/wave function of matter and energy). Here, your physics remains grossly predictive (Einstein’s equations that make the predictability of nuclear fusion and fission very predictable) but less and less predictive as smaller and smaller scales moving toward the Planck Length (an infinitely disappearing and receding distance that one can never cross)—yeah, all that. That stuff is basic to modern physics, but here’s what I’m asking you: doesn’t quantum mechanics, just like classical Newtonian physics described a time evolution of physical systems using a mathematical structure, the wave function? If so, the wave function is BOTH a certainty (Newtonian) AND a probability (Heisenberg) that the system will be found in a given state at a given time? But that scaling down, this probability grows more and more non determinable? And if that’s true, you then have to start predicting the effect on a system of the act of measuring the system? (‘the act of measuring destroys the measure’?) Thus, the uncertainty principle, and Schrödinger’s cat, and all that----
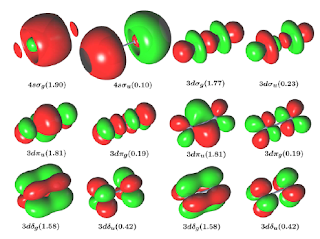 |
| the dynamism of quantum bonds! |
Okay, now here is my REAL question: since superconductivity and the introduction of computational theory, aren’t we seeing more and more that even though you physicists couldn’t drive classical predictive power from the macro level down into the sub micro level, that predictive power is now creeping up from micro to macro levels? Computational chemistry is using quantum theory to describe, predict, and even to synthesize outcomes of atomic orbitals, and angular momentum in CHEMICAL BONDS. Why is this happening, because computational chemistry is showing that even at the macro level (the molecular level) the bonds are not fixed, but are displaying a wave-particle sort of duality. The 'ball and stick' model of molecular bonds is in reaity far less fixed or predictable. The reality is vast collections, constantly changing, of nuclei surrounded by both circulating AND shifting, phasing, and vibrating clouds of electrons! Highly accurate predictions of chemical bonding behavior that we all learned in high school chemistry and that work very well, were to a great extent derived from experimentation and the observable results of experiments, not necessarily from computation. Since applying quantum principles to molecular theory (as opposed to experimental certainty) chemists have been able to create new, exotic, unpredicted bonds and thus new molecules that could not have been anticipated by classical chemistry. Or am I wrong?

No comments:
Post a Comment